Introduction to the Reasonings
Reasonings, the cognitive process of drawing conclusions or making inferences, lies at the heart of human cognition. It serves as a vital tool for decision-making, problem-solving, and understanding the world around us. This article aims to shed light on reasoning, its various types, and the cognitive intricacies that underlie this fundamental aspect of human thinking.
What Is Reasoning?
Reasoning encompasses the mental processes involved in forming judgments, evaluating evidence, and deriving conclusions based on available information. It allows individuals to make sense of complex data, identify patterns, and reach logical outcomes.
According to American Psychological Association (APA, 2018) Reasoning is thinking in which logical processes of an inductive or deductive character are used to draw conclusions from facts or premises. There two basic types – deductive reasoning & inductive reasoning.
Deductive Reasoning – the form of logical reasoning in which a conclusion is shown to follow necessarily from a sequence of premises, the first of which stands for a self-evident truth or agreed-upon data. In the empirical sciences, deductive reasoning underlies the process of deriving predictions from general laws or theories.
Inductive reasoning– the form of reasoning in which inferences and general principles are drawn from specific observations and cases. Inductive reasoning is a cornerstone of the scientific method in that it underlies the process of developing hypotheses from particular facts and observations.
Syllogistic reasoning, often associated with the work of Aristotle, involves drawing conclusions based on the relationship between categories. A syllogism comprises two premises and a conclusion, typically revolving around universal or particular statements about categories. Categorical syllogisms, the most well-known form, analyze how members of different categories relate to one another.
For example, a syllogism might state, “All A are B” and “All B are C,” concluding that “All A are C.” This form of reasoning requires identifying the middle term shared between the premises and determining whether a valid conclusion logically follows. Categorical syllogisms represent deductive logic in its purest form, as they allow no room for uncertainty if the premises are valid.
On the other hand, conditional reasoning focuses on “if-then” structures, where the outcome depends on certain conditions being met. This type of reasoning is integral to scientific inquiry, decision-making, and everyday problem-solving.
Conditional reasoning involves two key components: an antecedent (the “if” part) and a consequent (the “then” part). A valid conditional argument ensures that if the antecedent is true, then the consequent must also be true. Conditional reasoning is often tested through modus ponens (if P, then Q; P is true, so Q must be true) and modus tollens (if P, then Q; Q is false, so P must be false), which form the foundation for evaluating logical consistency.
Both syllogistic and conditional reasoning are essential tools in deductive logic. While syllogistic reasoning relies on category memberships to form conclusions, conditional reasoning is concerned with how specific conditions affect outcomes. Together, these forms of reasoning provide valuable insights into human cognition, offering a framework for understanding how we process information and make logical decisions.
Conditional Reasoning
Conditional reasoning is a critical type of deductive reasoning in which conclusions are derived from an if-then (conditional) proposition. This form of reasoning is fundamental in logic, mathematics, and everyday decision-making.
It revolves around the relationship between an antecedent (denoted as p) and a consequent (denoted as q). The essence of conditional reasoning is encapsulated by the proposition, “If p, then q,” which posits that if a certain condition (p) is met, then a specific result (q) follows. For instance, the statement “If students study hard, then they score high on their exams” is a classic example of conditional reasoning, where studying hard (p) leads to high scores (q).

Conditional Reasoning
This reasoning process is deductively valid, meaning it logically follows from the premises on which it is based. However, the deductive validity of a conclusion does not necessarily equate to its truthfulness. Deductive reasoning requires that both the premises and the conclusion are logically consistent, regardless of the factual accuracy of the premises (Cengage Learning, 2017).
Modus Ponens and Modus Tollens
Two central forms of conditional reasoning that are deductively valid are modus ponens and modus tollens. These are logical rules that govern how reasoners can draw conclusions from conditional propositions.
- Modus Ponens (Affirming the Antecedent)
Modus ponens is a form of argument where the antecedent is affirmed, and from this, the consequent is derived. This is expressed in the structure:
An example is, if you are a mother, then you have a child. You are a mother. Therefore, you have a child. This form of reasoning is deductively valid because the conclusion follows logically from the premises.
2. Modus Tollens (Denying the Consequent)
Modus tollens involves denying the consequent to infer the denial of the antecedent. The structure is:
For example, if you are a mother, then you have a child. You do not have a child. Therefore, you are not a mother. This is also deductively valid, as the conclusion logically follows from the negation of the consequent.
Deductive Fallacies in Conditional Reasoning
While modus ponens and modus tollens are logically sound, there are also deductive fallacies that arise when people misuse conditional propositions. Two common fallacies are denying the antecedent and affirming the consequent.
1.Denying the Antecedent
This fallacy occurs when a reasoner incorrectly assumes that denying the antecedent leads to the denial of the consequent. The structure is:
For example, if you are a mother, then you have a child. You are not a mother. Therefore, you do not have a child. This is a fallacy because not being a mother does not necessarily mean the individual does not have a child (Cengage Learning, 2017).
2. Affirming the Consequent
This fallacy occurs when the consequent is affirmed to infer the truth of the antecedent. The structure is:
For instance, if you are a mother, then you have a child. You have a child. Therefore, you are a mother. This is a fallacy because having a child does not necessarily imply that the person is a mother (they could be a father, for example).
The Wason Selection Task: Studying Conditional Reasoning
One of the most widely used experimental methods for studying conditional reasoning is the Wason Selection Task, developed by Peter Wason in the 1960s. This task presents participants with a set of four cards, each showing a letter on one side and a number on the other. The task involves testing a conditional proposition, such as “If a card has a consonant on one side, then it has an even number on the other side” (Wason, 1968).
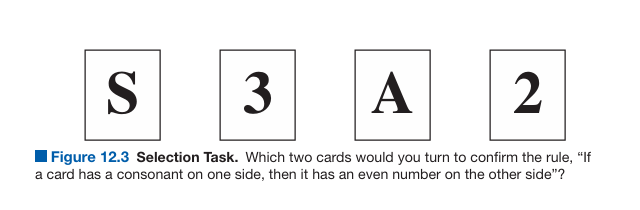
Wason Selection Task

Wason Selection Task (Sternberg & Sternberg)
Participants are instructed to turn over only those cards necessary to test the conditional statement. The correct strategy requires using both modus ponens (affirming the antecedent by turning over the consonant card) and modus tollens (denying the consequent by turning over the odd-number card). However, many participants fail to use the modus tollens strategy and instead incorrectly use the fallacies of affirming the consequent or denying the antecedent.
In studies, participants often perform well when affirming the antecedent, but many struggle with denying the consequent. For example, in the Wason Selection Task, participants frequently turn over cards that do not provide valid tests of the conditional proposition, such as those affirming the consequent (Wason & Johnson-Laird, 1970).
Conditional Reasoning in Everyday Life
Conditional reasoning is not just an abstract form of reasoning used in logic puzzles; Studies show that while many people can apply modus ponens in real-life scenarios, they often fail to recognize the importance of modus tollens. Furthermore, they frequently fall prey to logical fallacies when reasoning about real-world situations (Braine & O’Brien, 1991; O’Brien, 2004; Rips, 1988).
For example, in everyday contexts, people are often misled by the affirmation of the consequent fallacy. Consider the statement, “If you buy the textbook, you will get a $5 rebate.” Many people would infer that if they received the rebate, they must have bought the textbook, even though there could be other ways to obtain the rebate.
Similarly, the denial of the antecedent fallacy occurs when people assume that if they didn’t buy the textbook, they cannot get the rebate, even though the conditional statement does not exclude other possibilities (Rumain, Connell, & Braine, 1983).
Contextual Influences on Conditional Reasoning
The success of conditional reasoning often depends on the context in which it is presented. For instance, in a study by Griggs and Cox (1982), participants were asked to enforce a legal drinking age rule: “If a person is drinking beer, then the person must be over 19 years of age.” Given this context, participants performed significantly better on the Wason Selection Task, with 72% of participants choosing the correct cards (those testing modus ponens and modus tollens). This result contrasts sharply with their performance on the abstract version of the task, where no participant arrived at the correct conclusion.
These findings suggest that people reason more effectively when the conditional problem is embedded in a familiar, real-world context. Abstract reasoning problems, on the other hand, often lead to logical fallacies because participants fail to apply the appropriate logical structures (Griggs & Cox, 1982).
Moreover, personality traits such as distrust can influence performance on the Wason Selection Task. Mayo, Alfasi, and Schwarz (2014) found that individuals with higher levels of distrust were more likely to engage in negative hypothesis testing (using modus tollens) and, as a result, reached correct conclusions more frequently. Distrust seems to encourage a more critical and skeptical approach to reasoning, reducing the likelihood of taking information at face value.
Applications and Implications
The principles of conditional reasoning have broad applications across various domains, including law, medicine, and education. In law, for example, conditional reasoning is crucial in establishing legal precedents based on the relationship between conditions and outcomes. In medicine, it is used to make diagnostic decisions: “If the patient has symptom ppp, then they have disease qqq.” Misapplication of conditional reasoning, such as affirming the consequent, can lead to incorrect diagnoses or legal conclusions.
Educators can improve students’ reasoning skills by teaching them to recognize and avoid logical fallacies. While formal logic training can help, everyday reasoning can still be prone to fallacies, even after instruction (Cheng et al., 1986). Integrating real-world examples and focusing on modus tollens may enhance students’ ability to reason conditionally.
Syllogism
Categorical Syllogisms
Syllogistic reasoning is a type of deductive reasoning where conclusions are drawn from two premises. One common form is the categorical syllogism, which involves class membership and follows a specific structure. In categorical syllogisms:
- There are two premises, each making a statement about the relationship between categories.
- Each term represents members of a class and relates the categories through the use of universal or particular qualifiers.
For example-
Premise 1- All cognitive psychologists are pianists.
Premise 2- All pianists are athletes.
Conclusion- Therefore, all cognitive psychologists are athletes.
This syllogism is valid because the conclusion logically follows from the premises, even though the premises themselves may be factually false. To visualize the class memberships, logicians use circle diagrams that help clarify whether the conclusion follows logically. However, if the premises are untrue, the conclusion, though logically valid, may not reflect reality.
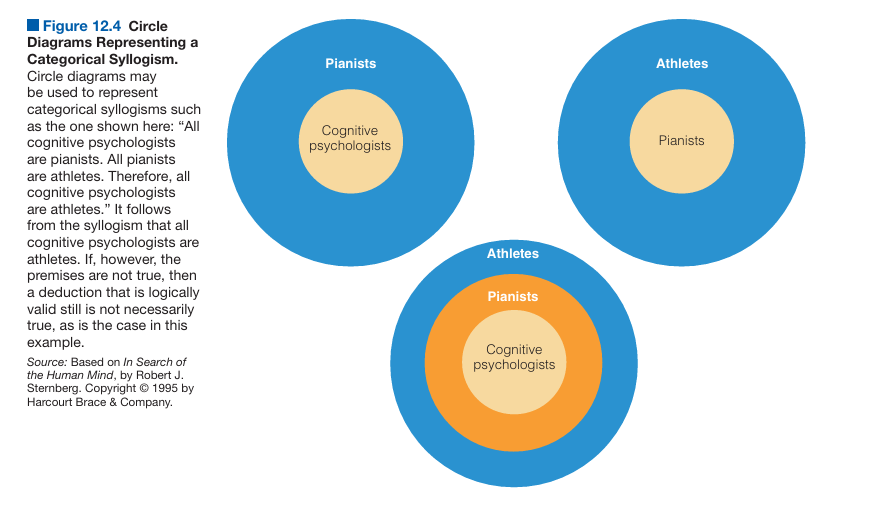
Categorical Syllogism
Types of Categorical Statements
- Universal Affirmative- “All A are B” (e.g., all dogs are animals).
- Universal Negative- “No A are B” (e.g., no dogs are cats).
- Particular Affirmative- “Some A are B” (e.g., some dogs are friendly).
- Particular Negative- “Some A are not B” (e.g., some dogs are not small).
In syllogisms, two particular premises or two negative premises often fail to lead to a logically valid conclusion. For instance, “Some cognitive psychologists are left-handed” and “Some left-handed people are smart” don’t lead to a valid conclusion about cognitive psychologists being smart.
Solving Syllogisms
People often use mental models to represent the premises. Mental models are internal representations that mirror the categories and relations described in the syllogism. Depending on the model used, conclusions may or may not be valid. For example, a mental model of “all artists are beekeepers” and “some beekeepers are clever” may lead to the invalid conclusion that some artists are clever, depending on how the reasoner imagines the overlap between categories.
Johnson-Laird’s research suggests that solving more complex syllogisms requires multiple mental models, each adding strain to the working memory. Problems that only need one model are easier to solve, while those requiring multiple models are more challenging and prone to error, especially if working memory is overwhelmed.
Categorical syllogisms are foundational to deductive reasoning, and understanding them is enhanced through visual aids like circle diagrams and mental models. However, the complexity of reasoning often depends on memory capacity and the number of models required to reach valid conclusions.
Application of Syllogisms
In psychology, syllogistic reasoning plays a crucial role in understanding how individuals process logical arguments and make decisions. It is often used to study cognitive processes, such as reasoning, problem-solving, and decision-making, by examining how people deduce conclusions from given premises. For example, psychologists may present participants with logical problems in the form of syllogisms to investigate the mental strategies they use to reach conclusions and to identify potential biases or errors in reasoning. This type of deductive reasoning also helps psychologists explore cognitive development and how reasoning skills evolve over time.
Moreover, syllogistic reasoning is applied in therapeutic settings, particularly in cognitive-behavioral therapy (CBT). Therapists help clients identify faulty syllogistic reasoning patterns that contribute to negative thought processes and behaviors. For instance, a client may form an illogical conclusion based on incorrect premises, such as “All people who fail are worthless; I failed at this task; therefore, I am worthless.” By addressing and restructuring these syllogisms, therapists can guide clients toward more balanced and rational thinking.
Additionally, syllogistic reasoning is used in the development of psychological assessments and experiments. Researchers employ it to design tasks that test logical reasoning abilities, such as determining whether conclusions drawn from two premises are valid or flawed. This is particularly useful in assessing cognitive deficits in individuals with neurological conditions, such as brain injuries or disorders that impair reasoning abilities. By analyzing syllogistic reasoning performance, psychologists can gain insights into a person’s cognitive functioning and develop appropriate interventions.
Overall, syllogistic reasoning in psychology not only aids in the study of cognitive processes but also has practical applications in therapy, assessments, and experimental research, making it a fundamental tool in understanding and improving human reasoning.
Conclusion to the Reasonings
Syllogistic reasoning and conditional reasoning, though distinct in their structure and applications, are both fundamental components of deductive logic. Syllogistic reasoning simplifies the relationships between categories, allowing individuals to draw straightforward conclusions from universal or particular premises. Conditional reasoning, on the other hand, introduces a more dynamic form of logic, where conclusions depend on the satisfaction of specific conditions. Each method demonstrates the capacity of the human mind to process complex logical structures, but also underscores the limitations that can arise, particularly when premises are ambiguous, invalid, or when working memory is taxed.
In syllogistic reasoning, errors can occur when the premises are not carefully evaluated, or when particular premises are involved, leading to confusion over the relationships between categories. Similarly, conditional reasoning can falter when individuals misinterpret the antecedent-consequent relationship or fail to recognize invalid logical forms, such as affirming the consequent or denying the antecedent. Despite these challenges, understanding both forms of reasoning enhances cognitive flexibility, enabling individuals to navigate a wide array of logical scenarios, from everyday decision-making to formal scientific reasoning.
Ultimately, the study of syllogistic and conditional reasoning provides valuable insights into how humans engage in deductive thought. It reveals not only the strengths of human logic but also the potential pitfalls that can arise from cognitive limitations. By exploring these reasoning processes, individuals can sharpen their critical thinking skills, improving their ability to draw sound conclusions in both theoretical and practical contexts.
References
Braine, M. D. S., & O’Brien, D. P. (1991). A theory of if: A lexical entry, reasoning program, and pragmatic principles. Psychological Review, 98(2), 182-203.
Cheng, P. W., Holyoak, K. J., Nisbett, R. E., & Oliver, L. M. (1986). Pragmatic versus syntactic approaches to training deductive reasoning. Cognitive Psychology, 18(3), 293-328.
Cengage Learning. (2017). Logic and reasoning. Cengage Learning.
Griggs, R. A., & Cox, J. R. (1982). The elusive thematic-materials effect in Wason’s selection task. British Journal of Psychology, 73(3), 407-420.
Mayo, R., Alfasi, N., & Schwarz, N. (2014). Distrust and the positive test heuristic: Dispositional and contextual distrust impairs performance on the Wason rule-discovery task. Journal of Experimental Psychology: General, 143(3), 985-990.
Matlin, M. W., & Farmer, A. (2019). Cognition (10th ed.). Wiley.
O’Brien, D. P. (2004). Conditionals and disjunctions in models of conditional reasoning. Thinking & Reasoning, 10(1), 45-51.
Rips, L. J. (1988). Reasoning and prototypes: Relations between logical and cognitive models. Advances in Psychology, 44, 247-270.
Rumain, B., Connell, J., & Braine, M. D. S. (1983). Conversational comprehension processes are responsible for reasoning fallacies in children as well as adults: If is not the biconditional. Developmental Psychology, 19(4), 471-481.
Sternberg, R. J., & Sternberg, K. (2006). Cognitive psychology (p. 178). Belmont, CA: Thomson/Wadsworth.
Wason, P. C. (1968). Reasoning about a rule. Quarterly Journal of Experimental Psychology, 20(3), 273-281.
Wason, P. C., & Johnson-Laird, P. N. (1970). Psychology of reasoning: Structure and content. Harvard University Press.
Subscribe to Careershodh
Get the latest updates and insights.
Join 15,051 other subscribers!
Niwlikar, B. A. (2024, October 24). Master 2 Insightful Types of Reasonings- Syllogistic and Conditional Reasoning. Careershodh. https://www.careershodh.com/types-of-reasonings/
