Problem Solving- Discover the 2 Insightful Types of Problems

Introduction

Problem solving is a fundamental cognitive process that we use to find solutions to difficult or complex issues (Matlin & Farmer, 2019). This process typically involves identifying a problem, generating a range of potential solutions, and implementing the most effective one.

Problem-solving can be broadly categorized into two types:

1. well-structured problems

2. Ill-structured problems,

each with distinct characteristics, strategies, and challenges.

1.Well-Structured Problems 

Well-structured problems, also known as well-defined problems, are those with a clear path to a solution. They feature well-defined initial and goal states, as well as explicit operations that move the problem solver from the initial state to the goal state. The clarity in the structure makes it easier for solvers to apply known rules or algorithms to arrive at a solution.

An example- calculating the area of a parallelogram—a task that requires the straightforward application of a formula to arrive at a correct solution.

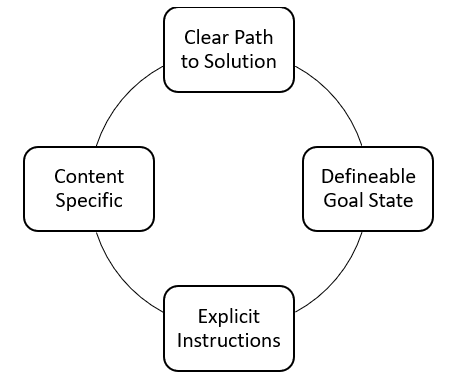
Characteristics of Well-Structured Problems

1. Clear Path to Solution

Well-structured problems typically offer a clear, predictable path to a solution because they follow established procedures. When the correct steps are followed, the solution is guaranteed. For instance, solving a mathematical equation, such as finding the roots of a quadratic equation, can be accomplished using a known algorithm like the quadratic formula (-b± b^2-4ac)/2a. This algorithm guarantees the correct solution if applied accurately.

For example, consider the problem of solving the equation (2x+3=7). The clear steps to solve this equation are: subtracting 3 from both sides and then dividing both sides by 2. This structured nature of the problem makes the path to the solution straightforward and easily repeatable, which is a hallmark of well-structured problems.

Research by Chi et al. (1988) highlights that novice problem solvers often struggle with ill-structured problems because they lack a clear path or algorithm. However, when presented with a well-structured problem like a mathematical equation, novices can generally solve it by following the prescribed steps.

2. Definable Goal State

In well-structured problems, the end goal is specific and unambiguous. The problem solver knows exactly what they are aiming to achieve, whether it’s finding a numerical solution, identifying a historical event, or locating a geographical feature. This clarity helps guide the problem-solving process and reduces confusion.

For example, solving the equation (2x+3=7) involves a clear goal—finding the value of (x). This definable goal state provides a direct pathway to the solution.

Mayer (1992) demonstrated that students are more successful when the goal state of a problem is clearly defined. Knowing exactly what they are trying to achieve allows students to apply appropriate strategies, unlike in ill-structured problems, where the goal may be vague or undefined.

3. Explicit Instructions

Well-structured problems offer explicit instructions, clearly defining how to approach the solution. This eliminates ambiguity, allowing the problem solver to focus solely on applying the steps or rules provided rather than interpreting the problem’s meaning. Explicit instructions give problem solvers the necessary information to guide their actions without needing to infer hidden steps or ambiguous requirements.

Consider a problem where you are asked to solve (2x+3=7). The instructions are explicit: find the value of \(x\) using basic operations like subtraction and division. This clarity ensures that there is no room for interpretation or uncertainty about the required steps. Sweller’s (1988) research on cognitive load theory highlights that explicit instructions reduce the mental effort required to understand the task, allowing problem solvers—especially novices—to focus on solving the problem rather than determining how to approach it.

4. Content-Specific

Well-structured problems are often context-specific, particularly in educational settings where problems are tied to specific subjects like mathematics, history, or geography. These problems require the application of domain-specific knowledge, such as solving a mathematical equation or identifying historical facts.

For example, solving (2x+3=7) clearly falls within the domain of mathematics, narrowing the scope and directing the problem solver to apply their mathematical knowledge. Siegler and Alibali (2005) found that students perform better on content-specific, well-structured problems because they can rely on previously learned information. Such problems are easier to solve since they do not require generating new strategies or dealing with ambiguity, allowing solvers to directly apply their learned knowledge to arrive at a solution.

Well Defined Problem

Case Analysis: Move Problems 

Move problems represent a well-studied subcategory of well-structured problems within cognitive psychology. These problems involve a sequence of actions that must be performed in a specific order to achieve a well-defined goal state. Although the path to the solution is structured, certain rules or constraints add complexity, limiting the options available for each move. The structured nature of move problems, coupled with their clear goal states, makes them ideal for studying problem-solving strategies and cognitive processes.

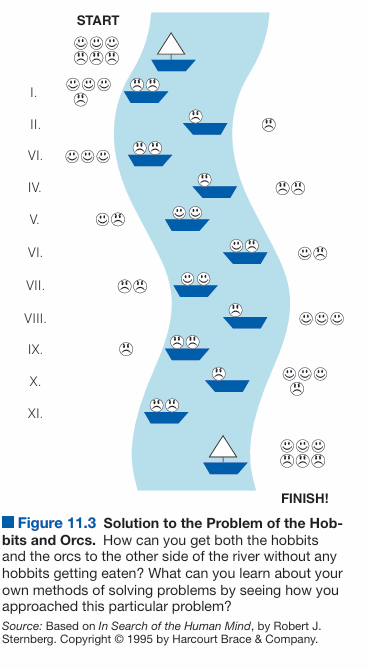
One famous example of a move problem is the “Hobbits and Orcs” puzzle. In this problem, three hobbits and three orcs must cross a river using a boat that can only carry two individuals at a time. The goal is to get all six characters safely across the river.

However, the constraints complicate the problem: at no point can orcs outnumber hobbits on either side of the river, or the orcs will attack and eat the hobbits. Additionally, the boat cannot move without at least one character on board.

Steps to Solve the Hobbits and Orcs Problem

1. The first challenge is determining how to move both hobbits and orcs across the river while maintaining a safe ratio between the two groups. Given the constraints, this problem requires strategic planning and foresight.
2. A common solution starts by having two orcs cross the river. One stays on the far side while the other returns with the boat. The process continues with another group of orcs or hobbits crossing and returning as needed.
3. Solving this problem requires more than trial and error. It involves mentally simulating the consequences of each move to avoid situations where the hobbits are outnumbered. This forces problem solvers to plan ahead and hold multiple intermediate states in mind, a cognitive task that requires working memory, planning, and cognitive flexibility.

Hobbits and Orcs

Cognitive Processes in Move Problems 

Move problems like the Hobbits and Orcs puzzle are ideal for studying several cognitive processes, including working memory, planning, and cognitive flexibility. These tasks require individuals to track the current state of the problem, mentally represent possible future moves, and continuously adjust their plan based on new information.

Working memory is crucial in holding multiple pieces of information—such as who is on each side of the river—and determining the next move. Planning plays a key role as solvers must think ahead and consider the consequences of each decision.

2.Ill-Structured Problems

Ill-structured problems, also called ill-defined problems, lack a clear path to a solution. These problems are often more complex and ambiguous than well-structured problems, with no obvious or prescribed method for finding a solution.

An example – Deciding which house to buy when each potential option has both advantages and disadvantages. Unlike well-structured problems, there is no single “correct” solution, and decision-making involves weighing multiple variables and considering various trade-offs.

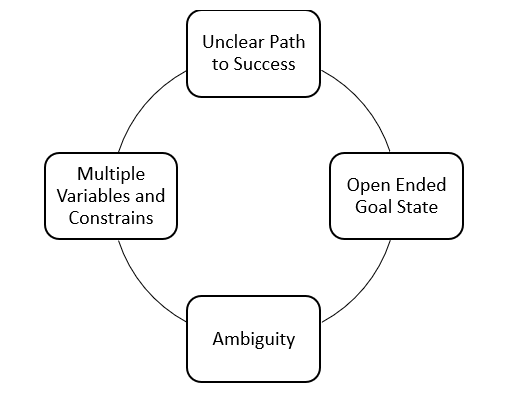
Characteristics of Ill-Structured Problems

1. Unclear Path to Solution

The most defining feature of ill-structured problems is that there is no clear or predetermined set of steps to solve them. Unlike well-structured problems, where algorithms or formulas guide the solver, ill-structured problems require solvers to devise their own approach. This uncertainty forces individuals to engage in trial and error, brainstorming, and creative problem-solving.

A real-world example of an ill-structured problem is addressing climate change. There is no clear-cut algorithm or single solution to reduce global carbon emissions. Instead, multiple solutions exist, such as transitioning to renewable energy, implementing carbon taxes, or promoting energy efficiency. However, each solution requires weighing political, economic, and social factors, with success depending on how well these factors are managed.

2. Open-Ended Goal State

In ill-structured problems, the goal state is often not as specific or unambiguous as in well-structured problems. Different solvers may interpret the problem differently, leading to various conceptions of what constitutes success. As a result, the goal state becomes more subjective, and the “solution” can differ based on the individuals, groups, or contexts involved.

For instance, what does success in addressing climate change look like? Some might define success as limiting global warming to 1.5°C above pre-industrial levels, in line with the Paris Agreement. Others might focus on more localized objectives, such as ensuring coastal cities are prepared for rising sea levels or minimizing biodiversity loss. These different goals highlight the open-ended nature of ill-structured problems.

Jonassen (1997) argued that ill-structured problems do not have clear-cut solutions and are often evaluated based on criteria that vary across contexts. Success depends on the solver’s judgment and the goals they prioritize. In educational settings, this is seen in open-ended projects where students must propose solutions to real-world problems, with each solution reflecting different values and interpretations.

3. Ambiguity

Ill-structured problems are characterized by ambiguity, meaning that the information provided is often incomplete, conflicting, or unclear. This vagueness forces solvers to interpret the information, make assumptions, and clarify the problem before attempting to solve it. Ambiguity adds to the complexity, as solvers must first define what the problem actually is.

For example, climate change projections vary depending on the models and assumptions used. The ambiguity of future climate scenarios forces decision-makers to weigh uncertain predictions and formulate strategies that can adapt to a wide range of possible outcomes.

Similarly, in the corporate world, ill-structured problems like market expansion often require managers to make decisions based on incomplete data about competitors and consumer behavior. Therefore, ambiguity complicates the problem-solving process by introducing uncertainties that are difficult to resolve.

Research by Dörner and Funke (2017) on complex problem-solving highlighted that ambiguity increases cognitive load and can lead to decision-making errors. Solvers may either over-simplify the problem by ignoring key variables or become overwhelmed by the ambiguity, leading to indecision or poorly thought-out solutions.

4. Non-Linear Problem-Solving Process

The problem-solving process for ill-structured problems is often non-linear, requiring solvers to revisit earlier stages of the problem, redefine the problem, or reconsider previous solutions as new information emerges. This iterative process contrasts with the step-by-step, linear approach used for well-structured problems.

For instance, a government attempting to address rising healthcare costs may start by exploring different models of healthcare delivery. However, as they gather new data—perhaps on the effectiveness of existing systems in other countries—they might revise their goals and explore new options. This non-linear, recursive process of revisiting earlier stages of the problem adds to the complexity and requires solvers to maintain flexibility in their thinking.

Research by Newell and Simon (1972) on problem-solving as search processes showed that ill-structured problems often involve navigating a vast problem space with no clear starting point or end point. Solvers must continuously refine their approach based on new information and feedback, which requires a higher degree of cognitive flexibility than well-structured problems.

Ill Defined Problem

Case Study: Tackling Climate Change 

A classic example of an ill-structured problem is the issue of climate change. Climate change is a multifaceted global issue that requires actions on numerous fronts—technological, political, economic, and social. No single solution exists that can eliminate the problem entirely, and each approach has its own trade-offs. Tackling climate change requires decision-makers to consider scientific evidence, economic factors, political realities, and public opinion, making it a quintessential ill-structured problem.

• Unclear Path- There is no one-size-fits-all approach to solving climate change. Different strategies such as implementing renewable energy sources, introducing carbon taxes, or investing in climate mitigation technologies are often debated, with no consensus on which method is best. As a result, policy-makers must engage in complex decision-making processes, weighing various environmental, economic, and social factors.
• Ambiguous Goal State- The goal of tackling climate change is also not entirely clear. While most agree that limiting global warming to 1.5°C or 2°C above pre-industrial levels is critical, there are multiple interpretations of what success might look like at regional, national, and global levels. Additionally, certain countries or stakeholders may prioritize different goals, such as reducing the impact on their economy or preserving biodiversity, making the definition of success subjective.
• Non-Linear Problem-Solving Process- Addressing climate change also requires a non-linear approach, as new scientific data continuously emerges, influencing policy decisions and potentially changing the path forward. Governments may implement a policy only to discover later that it is not effective, leading to the need to revise or abandon it. This dynamic, adaptive problem-solving process is typical of ill-structured problems where conditions and information change frequently.

Cognitive Processes Involved in Ill-Structured Problems

Solving ill-structured problems requires higher-order cognitive processes such as critical thinking, creative problem-solving, and the ability to handle ambiguity. These processes are essential for navigating complex, real-world problems that do not have clear solutions. Unlike well-structured problems, where solvers can rely on established algorithms or heuristics, ill-structured problems demand more flexible, adaptive thinking.

1. Handling Ambiguity- One of the key cognitive processes involved in solving ill-structured problems is the ability to tolerate and manage ambiguity. This involves dealing with incomplete or contradictory information and still being able to make decisions. Dörner (1996) argued that individuals who are more comfortable with ambiguity are better at navigating complex problems and finding innovative solutions.
2. Critical Thinking and Reflection- Critical thinking is essential when working with ill-structured problems, as solvers must continually evaluate the information at hand, question their assumptions, and consider multiple perspectives. Schön (1983) introduced the concept of “reflection-in-action,” where problem solvers continuously assess their strategies and adjust their thinking in response to new challenges and changing circumstances.
3. Metacognition- Metacognition, or thinking about one’s own thinking, plays a vital role in solving ill-structured problems. Effective problem solvers frequently monitor their progress, recognize when they need to change their approach, and evaluate the effectiveness of different strategies. Flavell (1979) emphasized that successful problem solvers have strong metacognitive skills, allowing them to reflect on their thought processes and make adjustments as needed.

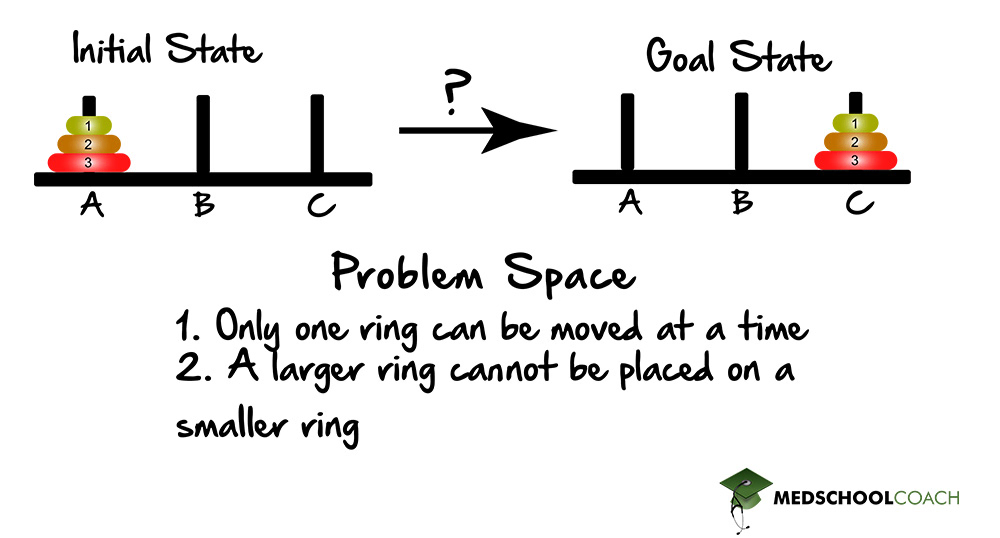
Isomorphic Problems

Isomorphic problems are those that share a formal structure despite differing in content. This means that the underlying principles or strategies used to solve one problem can often be applied to another problem with a similar structure, even if the specific details differ.

For instance, the hobbits and orcs problem and the missionaries and cannibals’ problem are isomorphic because they both involve constraints that must be managed to avoid a negative outcome (e.g., cannibals eating missionaries or orcs attacking hobbits) while transporting individuals across a river. The structural similarity lies in the need to balance groups to prevent adverse outcomes, even though the specific characters and scenarios differ. Similarly, word games like Scrabble and Boggle are isomorphic because they both involve forming words from a set of letters, although the rules and formats of the games vary.

Problem Representation

Problem representation involves translating the elements of a problem into a different format to make it easier to solve. The choice of representation can significantly impact problem-solving effectiveness.

Tower of Hanoi

1. Symbols- using symbols can simplify abstract problems by translating them into mathematical formulas. For instance, solving a problem involving ages can be made easier by representing the ages with symbols and creating equations (e.g., m=2s−10m = 2s – 10m=2s−10). Research indicates that errors in symbol representation, such as misinterpreting roles or oversimplifying, can hinder problem-solving (Mayer, 2004; Fisher et al., 2011).
2. Matrices- Matrices are useful for problems with categorical information. They organize data into rows and columns, making it easier to track relationships and solve complex problems. Studies show that using matrices can improve problem-solving accuracy, as seen in problems involving hospital room assignments where students who used matrices were more successful (Schwartz, 1971).
3. Diagram- Diagrams provide a visual representation of information, which can simplify understanding and problem-solving. For example, hierarchical tree diagrams and graphical representations can clarify relationships between items, helping to solve problems like the Buddhist monk problem by visually illustrating when and where events intersect (Novick & Morse, 2000; Grant & Spivey, 2003).
4. Visual Image- visual imagery allows for abstract problem representation by creating mental images of the problem scenario. This method can help in understanding and solving problems by bypassing traditional representations and providing a different perspective (Koestler, 1964; Pylyshyn, 2006).

Conclusion 

Well-structured and ill-structured problems represent two ends of the problem-solving spectrum, each requiring different cognitive processes and strategies. Well-structured problems are easier to navigate due to their clear goal states, explicit instructions, and established paths to solutions. In contrast, ill-structured problems are more complex, ambiguous, and open-ended, requiring solvers to engage in critical thinking, handle uncertainty, and adapt their strategies as new information emerges. By understanding the distinctions between these types of problems, educators, psychologists, and problem solvers can better prepare for the unique challenges each presents.

The study of problem-solving processes provides insight into how we approach various tasks in our everyday lives, from simple calculations to global challenges like climate change. As cognitive psychology continues to evolve, new research will shed light on how we can optimize our problem-solving abilities across both well-structured and ill-structured problems, ultimately enhancing our capacity to tackle the increasingly complex problems of the modern world.

References

Chi, M. T. H., Glaser, R., & Rees, E. (1982). The role of the initial state in problem solving. Journal of Experimental Psychology: General, 111(2), 265-290. https://doi.org/10.1037/0096-3445.111.2.265

Mayer, R. E. (1992). Thinking, problem solving, cognition (2nd ed.). W.H. Freeman and Company.

Sweller, J. (1988). Cognitive load during problem solving: Effects on learning. Cognitive Science, 12(2), 257-285. https://doi.org/10.1016/S0364-0213(88)80023-5

Siegler, R. S., & Alibali, M. W. (2005). Children’s thinking: Cognitive development and individual differences. Prentice Hall.

Sternberg, R. J., & Sternberg, K. (2006). Cognitive psychology (p. 178). Belmont, CA: Thomson/Wadsworth.

Galotti, K. M. (2018). Cognitive psychology in and out of the laboratory. Thomson Brooks/Cole Publishing Co.

Jonassen, D. H. (1997). Instructional design models for well-structured and ill-structured problem-solving learning outcomes. Educational Technology Research and Development, 45(1), 65-94. https://doi.org/10.1007/BF02299613

Matlin, M. W., & Farmer, A. (2019). Cognition (10th ed.). Wiley.

Shin, J., Jonassen, D. H., & McGee, S. (2003). Predicting problem-solving performance in ill-structured domains. International Journal of Artificial Intelligence in Education, 13(2), 125-141.

Fisher, R., Duffy, T. M., & Heffernan, N. T. (2011). The impact of representation on problem-solving strategies. Journal of Educational Psychology, 103(2), 283-296. https://doi.org/10.1037/a0022295

Grant, A., & Spivey, M. (2003). Visualizing problems: The role of diagrams in problem-solving. Cognitive Psychology, 47(3), 180-196. https://doi.org/10.1016/S0010-0285(03)00020-2

Koestler, A. (1964). The act of creation. Viking Press.

Novick, L. R., & Morse, R. S. (2000). Representational changes in problem solving. Journal of Experimental Psychology: Learning, Memory, and Cognition, 26(1), 136-153. https://doi.org/10.1037/0278-7393.26.1.136

Pylyshyn, Z. W. (2006). The role of mental imagery in cognitive science. Cognitive Science, 30(5), 713-736. https://doi.org/10.1207/s15516709cog0000_68

Schwartz, J. (1971). Using matrices to solve problems in mathematics. Educational Studies in Mathematics, 2(4), 329-340. https://doi.org/10.1007/BF00378535